Cálculo Numérico I (2012)
Section outline
-
Profesor
José Javier Segura Sala
Departamento de Matemáticas, Estadística y Computación
Palabras Clave de la Asignatura
floating point arithmetic, Numerical Analysis, integración numérica, Ecuaciones no lineales, condicionamiento y estabilidad, Interpolación, numerical quadrature, condition and stability, nonlinear equations, aritmética de punto flotante, Cálculo numérico, interpolation
-

Datos identificativos de la Asignatura
-
Asignatura: Cálculo Numérico I
-
Código: G98
-
Departamento / Área: Departamento de Matemáticas, Estadísitica y Computación
-
Título: Grado en Matemáticas
-
Centro: Facultad de Ciencias
-
Créditos ECTS: 6
-
Idioma de impartición: Español
-
Profesor responsable: Jose Javier Segura Sala
Programa de la asignatura
1. Introducción al análisis numérico
- 1.1 Aritmética computacional. Estándar de punto flotante.
- 1.2 Condicionamiento de un problema. Estabilidad de los métodos numéricos. Ejemplos.
- 1.3 Coste computacional y eficiencia. Ejemplos.
- 1.4 Software y librerías matemáticas.
2. Resolución numérica de ecuaciones no lineales
- 2.1 Introducción.
- 2.2 Método de bisección.
- 2.3 Método de la secante.
- 2.4 Método de Newton-Raphson.
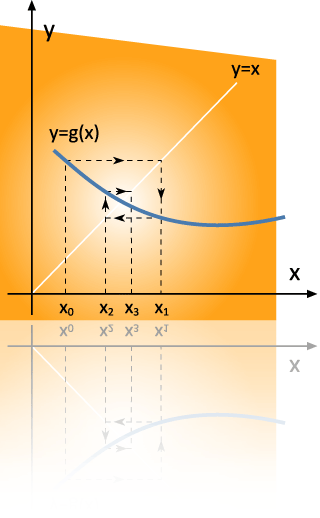
- 2.5 Métodos de punto fijo.
- 2.6 Raíces de polinomios
- 2.7 Introducción a la resolución de sistemas no lineales.
3. Interpolación y aproximación de funciones
- 3.1 Interpolación de Lagrange y teorema del resto.
- 3.2 Interpolación mediante diferencias divididas.
- 3.3 Interpolación de Hermite.
- 3.4 Interpolación de Chebyshev. Propiedades.
- 3.4 Interpolación por funciones spline.
4. Derivación e integración numérica
- 4.1 Fórmulas interpolatorias de derivación.
- 4.2 Fórmulas interpolatorias de integración. Fórmulas de Newton-Cotes simples y compuestas.
- 4.3 Introducción a la integración gaussiana.
- 4.4 Introducción a la cuadratura adaptativa.
-
-

Básica
-
K. Atkinson, Elementary Numerical Analysis, John Wiley & Sons, 1993.
-
R.L. Burden, J. D. Faires, Análisis Numérico, Grupo Editorial Iberoamérica,1985.
Complementaria
- F.S. Acton, Numerical Methods that work, The Mathematical Association of America, 1990.
- S.D.Conte, S. D., de Boor, C., Elementary Numerical Analysis (An Algorithmic Approach), McGraw-Hill, 1981.
-
-
-
-
-

Ejemplo de examen
Criterios de evaluación
MÉTODOS DE EVALUACIÓN "CÁLCULO NUMÉRICO I"
Descripción
Tipología
Evaluación final
Recuperación
%
Controles de prácticas en el laboratorio
Evaluación en laboratorio
No
Si
40%
-
Calificación mínima: 0,00.
-
Duración: Aproximadamente dos horas cada control
- Fecha realización: A lo largo del cuatrimestre
- Condiciones recuperación: Se puede recuperar mediante examen final de prácticas
Examen final
Examen escrito
Sí
Sí
45%
-
Calificación mínima: 0,00.
-
Duración: Tres horas aproximadamente
-
Fecha realización: Final del cuatrimestre
TOTAL
100%
OBSERVACIONES:
Cada alumno podrá individualmente decidir si desea que la parte práctica se evalúe únicamente mediante examen, en cuyo caso se examinará al alumno sobre contenidos prácticos tras la realización del examen final ordinario. En ese caso, tras el examen final se realizaría un examen práctico de una hora de duración, que sustituiría al 40% correspondiente a los controles de prácticas de la evaluación continua. Eso se aplica tanto a la convocatoria de Junio como a la de Septiembre (las notas de prácticas se mantienen para la convocatoria de Septiembre si así lo desea el alumno).
-
-







