Matemáticas Generales (2011)
Topic outline
-
Profesores
Patricia Gómez García
José Antonio Álvarez García
Departamento de Matemática Aplicada y CIencias de la Computación
En esta asignatura se estudian los principios básicos del Álgebra Lineal (vectores y matrices) y del Cálculo Diferencial e Integral (tanto en una variable como en varias). Se completa el programa con nociones básicas sobre sucesiones y series numéricas, haciendo especial hincapié en las progresiones aritméticas y geométricas.
Los objetivos principales de la asignatura son:
-saber utilizar las herramientas matemáticas necesarias para resolver problemas vinculados con la actividad económica y empresarial.
-saber aplicar herramientas informáticas que permitan la resolución e interpretación de problemas matemáticos.Palabras Clave de la Asignatura
Cálculo matricial, gráfica de una función, continuidad, derivabilidad, sistemas de ecuaciones lineales, progresión geométrica, funciones reales de una variable, espacios vectoriales, diagonalización, Integral de Riemann, progresión aritmética
-

Datos identificativos de la Asignatura
-
Asignatura: Matemáticas Generales
-
Código: G350
-
Departamento / Área: Matemática Aplicada y Ciencias de la Computación
-
Título: Grado en Economía
-
Tipo: Básica
-
Centro: Facultad de Ciencias Económicas y Empresariales
-
Créditos ECTS: 6
-
Curso / Cuatrimestre: 1 / 1
-
Idioma de impartición: Español
-
Profesora responsable: María Patricia Gómez García
-
Profesor colaborador: José Antonio Álvarez García / José Manuel López Camus
Programa de la asignatura
Bloque Temático 1: Los números
- Números naturales, enteros y racionales
- El número real
- Intervalos
- Valor absoluto y propiedades
Bloque Temático 2: Álgebra Lineal
Matrices y Sistemas de Ecuaciones Lineales- Matrices
- Determinantes
- Rango
- Sistemas de ecuaciones lineales
Espacios vectoriales- El espacio vectorial IRn
- Subespacio vectorial
- Dependencia e independencia lineal
- Sistema generador. Base
Aplicaciones Lineales y Diagonalización- Aplicaciones lineales
- Expresión matricial de una aplicación lineal
- Diagonalización
Bloque Temático 3: Funciones reales de una variable real
- Funciones reales de una variable real
- Límite de una función real
- Continuidad de una función real
Bloque Temático 4: Cálculo diferencial de funciones reales de una variable
Derivadas- El concepto de derivada.
- Relación entre continuidad y derivabilidad.
- Función derivada
- Operaciones con derivadas
- Derivación de las funciones elementales
- Propiedades de las funciones derivables
- Regla de L'Hôpital
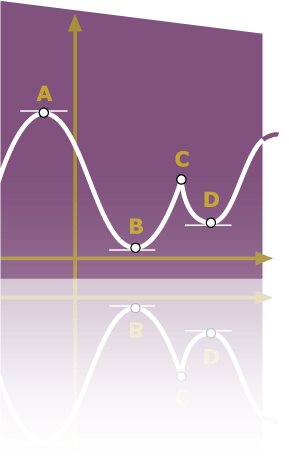
Estudio de la gráfica de una función- Crecimiento y decrecimiento
- Extremos absolutos y relativos
- Concavidad y convexidad
- Asíntotas
- Dibujo de la curva y=f(x)
Bloque Temático 5: Sucesiones y series de números reales
- Sucesiones de números reales. Límite de una sucesión. Cálculo de límites
- Series de números reales
- Progresiones aritméticas y geométricas. Series geométricas
Bloque Temático 6: Introducción al cálculo integral
- Integral de Riemann
- Propiedades
- Primitiva de una función. Integral indefinida
- Integrales inmediatas
- Relación entre las integrales indefinidas y las definidas
-
-

- 1. Barbolla, R. y Sanz, P. (1998). Álgebra lineal y teoría de matrices. Ed. Prentice Hall.
- 2. Bradley, G. L. y Smith, K. J. (1998). Cálculo de una variable, I. Ed. Prentice Hall.
- 3. Bradley, G. L. y Smith, K. J. (1998). Cálculo de varias variables, II. Ed. Prentice Hall.
- 4. Caballero, R. E., Calderón, S. y Galache, T. P. (2000). Matemáticas aplicadas a la economía y a la empresa. 434 ejercicios resueltos y comentados. Ed. Pirámide
- 5. Granero Rodríguez, F. (1991). Ejercicios y problemas de cálculo. Ed. Tebar-Flores.
- 6. Grossman, S. I. (1997). Álgebra lineal. Ed. McGraw-Hill.
- 7. Hernández, E (1999). Álgebra y geometría. Ed. Addison-Wesley/U.A.M.
- 8. Hoffmann, L. D. y Bradley, G. L. (1998). Cálculo para administración, economía y ciencias sociales. Ed. McGraw-Hill.
- 9. Kolman, B. (1999). Álgebra lineal con aplicaciones y Matlab. Ed. Prentice Hall.
- 10. Kolman, B. y Hill, D. R. (2006). Álgebra lineal. Ed. Pearson Educación de México.
- 11. Martínez Salas, J. (1992). Elementos de matemáticas. Ed. Lex Nova.
- 12. San Millán, M. A. y Viejo, F. (1992). Introducción a la Economía Matemática. Ed. Pirámide.
- 13. Sanz, P, Vázquez, F. J. y Ortega, P. (1998). Álgebra lineal. Cuestiones, ejercicios y tratamiento en Derive(R). Ed. Prentice Hall.
- 14. Sydsaeter, K. y Hammond, P. J. (1996). Matemáticas para el análisis económico. Ed. Prentice Hall.
-

Bloque Temático 1: Los números
- MC-F-001. Los números
Bloque Temático 2: Álgebra Lineal
Bloque Temático 3: Funciones reales de una variable real
- MC-F-005. Funciones reales de una variable real
Bloque Temático 4: Cálculo diferencial de funciones reales de una variable
Bloque Temático 5: Sucesiones y series de números reales
- MC-F-008. Sucesiones y series de números reales.
Bloque Temático 6: Introducción al cálculo integral
- MC-F-009. Introducción al Cálculo Integral
-

- PE-F-001. Examen enero 2011
Criterios de Evaluación
Las actividades de evaluación tienen como objetivo medir las competencias genéricas vinculadas a la asignatura:
1) Cooperar. La resolución en grupo de problemas matemáticos busca medir la capacidad del alumno para integrarse en un equipo de trabajo y contribuir al éxito de la tarea encomendada.
2) Resolver. Esta competencia se evaluará mediante las siguientes actividades:
- - Realización de tests en el Aula Virtual.
- - Resolución de problemas.
- - Examen final.
Con estas tres actividades, se busca medir la capacidad que el alumno tiene de abordar y resolver un problema matemático con la ayuda de los conocimientos adquiridos en las clases teóricas y prácticas. Además, en todas las pruebas y ejercicios escritos se valorará la calidad del desarrollo matemático y la claridad y corrección de las explicaciones y razonamientos que conlleva. No se tendrán en cuenta, por el contrario, los resultados dados sin justificación.
3) Utilizar software. En las sesiones prácticas en el aula de informática se valorará la asistencia y el rendimiento en la realización de los ejercicios propuestos. Las pruebas de evaluación planteadas tienen el objetivo de valorar la capacidad del alumno a la hora de aplicar las herramientas informáticas aprendidas a la resolución de problemas matemáticos.
La forma de evaluar se detalla a continuación:
- Resolución de problemas en grupos: al finalizar cada tema se propondrá a los alumnos, en una clase práctica, la resolución de varios problemas que deberán entregar durante esa sesión. La nota máxima que se puede obtener en cada sesión es de 1 punto. La nota final de esta actividad será la media de todas las calificaciones obtenidas durante el cuatrimestre.
- Realización de tests en el Aula Virtual: en diferentes días a lo largo del cuatrimestre y en fechas previamente indicadas, se convocará a los alumnos en el aula de informática para que en un periodo de tiempo limitado realicen un test a través del Aula Virtual. Cada test realizado se puntuará con un máximo de 1. La nota final de esta actividad será la media de todas las calificaciones obtenidas en los tests durante el cuatrimestre. Aquellos alumnos que lo deseen, tienen la opción recuperar esta nota respondiendo en la convocatoria de septiembre a un test escrito que abarcará todo el temario.
- Prácticas con software matemático. Se realizarán varias sesiones en el aula de informática en las que el alumno irá aprendiendo a manejar el software propuesto, para así poder aplicarlo al estudio de los conceptos matemáticos que se van viendo paralelamente en las clases teóricas y prácticas. Durante estas sesiones se deberán resolver ejercicios matemáticos con la ayuda del programa y deberán entregarse al finalizar las mismas. En cada una de estas clases se puede obtener una nota máxima de 0.5 puntos, siendo la nota final de esta actividad la media de las calificaciones obtenidas en cada sesión.
- Prueba de evaluación de software matemático: a lo largo del curso y en fechas previamente indicadas se convocará a los alumnos a una o dos pruebas de evaluación en el aula de informática, en las que deberán resolver varios ejercicios con la ayuda del software. La nota máxima que se puede obtener en cada una de estas pruebas es de 0.5. Si se realizan dos pruebas, la nota final de esta actividad será la media de las dos calificaciones obtenidas. Aquellos alumnos que lo deseen, tienen la opción recuperar esta nota en la convocatoria de septiembre respondiendo por escrito a una serie de preguntas sobre el manejo del software.
- Resolución de problemas: tras finalizar cada tema, se planteará al alumno, en una clase práctica, la resolución de varios problemas, que deberá realizar de forma individual y entregar finalizada dicha clase. Cada una de estas actividades se valorará con un máximo de 1 punto. La nota final de esta actividad será la media de las calificaciones obtenidas durante el cuatrimestre.
- Examen final: se realizará en febrero y consistirá en la contestación a preguntas teórico-prácticas y en la resolución de problemas. Es recuperable en septiembre y su nota máxima en ambas convocatorias es de 6 puntos.
Así pues, a lo largo del cuatrimestre el alumno puede obtener un máximo de 4 puntos que sumados a la nota que se obtenga en el examen final, bien en febrero o en septiembre, (que será de 6 puntos como máximo), constituye la calificación final del curso.
La prueba final en la convocatoria de septiembre se compone de:
- -el examen de recuperación de febrero, valorado con 6 puntos.
- -un test escrito, valorado con 1 punto, para aquellos alumnos que quieran mejorar la nota obtenida en los tests durante el cuatrimestre.
- -varias preguntas por escrito sobre el manejo del software, valoradas con 0.5 puntos, para los alumnos que quieran mejorar la nota obtenida durante el cuatrimestre en las pruebas de evaluación correspondientes.
Tanto en cualquiera de las pruebas de evaluación propuestas a lo largo del cuatrimestre como en los exámenes finales de febrero y septiembre, ante la utilización de cualquier método fraudulento se aplicará lo establecido en el capítulo XVI del Reglamento de los Procesos de Evaluación en la Universidad de Cantabria.
-

 Aquí puede descargarse la Guía de Aprendizaje en formato pdf
Aquí puede descargarse la Guía de Aprendizaje en formato pdf
-

Patricia Gómez García
Departamento de Matemática Aplicada
y Ciencias de la Computación
Más Información

José Antonio Álvarez García
Departamento de Matemática Aplicada
y Ciencias de la Computación
Más información
Universidad de Cantabria