Curso: Sistemas y Máquinas Fluido Mecánicas (2015)

Sistemas y Máquinas Fluido Mecánicas (2015)

Colapsar todo Expandir todo

sistemas_maquinas_fluido_mecanicas

Profesores

Carlos J. Renedo Estébanez

Inmaculada Fernández Diego

Félix Ortíz Fernández

Juan Carcedo Haya

Departamento de Ingeniería Eléctrica y Energética

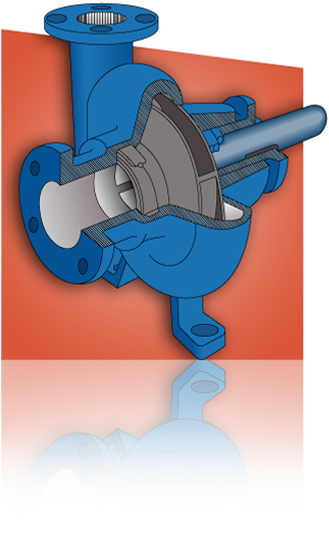
En esta asignatura se empiezan estudiando las máquinas hidráulicas propias de la ingeniería industrial: bombas y turbinas hidráulicas. Finalmente se desarrollan los sistemas neumáticos e hidráulicos de uso industrial.

This course will start studying the characteristics of hydraulic machines, pumps and turbines. Finally the pneumatic and hydraulic systems are developed for industrial use.

Palabras Clave de la Asignatura

Ventiladores, Pneumatics, Compressors, Neumática, Hydraulics, Turbines, Fans, Pumps, Bombas, Compresores, Hidráulica, Turbinas Hidráulicas.

Programa

programa

Datos identificativos de la Asignatura

Asignatura: Sistemas y Máquinas Fluido Mecánicas
Código: G750
Departamento / Área: Departamento de Ingeniería Eléctrica y Energética
Título: Grado en Ingeniería Mecánica
Centro: Escuela Técnica Superior de Ingenieros Industriales y de Telecomunicación
Créditos ECTS: 6
Idioma de impartición: Español
Profesor responsable: Carlos J. Renedo Estébanez
Otros profesores: Inmaculada Fernández Diego, Juan Carcedo Haya y Félix Ortiz Fernández

Programa de la asignatura

Bloque Temático I. Máquinas de fluidos incompresibles

Introducción.
Ecuación de Euler.
Bombas centrífugas:
- Características.
- Alturas.
- Clasificación.
- Curvas características.
- Instalación.
- Acoplamientos.
- Potencias, rendimientos y pérdidas.
- Golpe de ariete y cavitación.
- Leyes de semejanza.
- Número específico de revoluciones.
- Número de alabes.
- Punto de Funcionamiento.

Bombas de desplazamiento positivo:
- Generalidades.
- Tipos.

Turbinas hidráulicas:
- Generalidades.
- Turbinas Pelton.
- Turbinas Francias.
- Turbinas Kaplan.
- Estudio de turbinas hidráulicas.

Bloque Temático II. Máquinas de fluidos compresibles

Compresores:
- Tipos.

Ventiladores:
- Generalidades.
- Curvas características.
- Funcionamiento.
- Acoplamiento.
- Selección.

Representación de grafos.
Algoritmos básicos en grafos.

Bloque Temático III. Neumática e hidráulica

Introducción.
Fluidos de trabajo y su tratamiento.
Red de distribución del fluido de trabajo.
Elementos de trabajo y gobierno.
Diseño de circuitos.
Introducción a electro hidráulica/neumática.

Bibliografía

bibliografia

Básica

C. Mataix & Dossat: «Turbomáquinas Hidráulicas».
E. Camicer Royo & G. Gili: «Aire comprimido» (3 volúmenes).
J. Pelaez Vara, E. García Maté & Dossat: «Neumática Industrial».
A. Serrano Nicolas: «Oleohidraúlica». McGraw-Hill.

Materiales de Clase

materiales

Bloque I. Máquinas de fluidos incompresibles

MC-F-001. Tema 1. Introducción a las máquinas hidráulicas.
MC-F-002. Tema 2.1. Generalidades de las bombas hidráulicas.
MC-F-003. Tema 2.2.1. Bombas centrífugas I.
MC-F-004. Tema 2.2.2. Bombas centrífugas II.
MC-F-005. Tema 2.2.3. Bombas centrífugas III.
MC-F-006. Tema 2.2.4. Bombas centrífugas IV.
MC-F-007. Tema 2.2.5. Bombas centrífugas V.
MC-F-008. Tema 2.2.6. Bombas centrífugas VI.
MC-F-009. Tema 2.2.7. Bombas centrífugas VII.
MC-F-010. Tema 2.3. Bombas volumétricas.
MC-F-011. Tema 3.1. Generalidades de las turbinas hidráulicas.
MC-F-012. Tema 3.2. Turbinas Pelton.
MC-F-013. Tema 3.3. Turbinas Francis.
MC-F-014. Tema 3.4. Turbinas Kaplan.
MC-F-015. Tema 3.5. Estudio de turbinas hidráulicas.

Bloque II. Máquinas de fluidos compresibles

MC-F-016. Tema 4. Ventiladores.
MC-F-017. Tema 5.1. Compresores: generalidades y clasificación I.
MC-F-018. Tema 5.2. Compresores: clasificación II y teoría de la compresión.

Bloque III. Neumática e hidráulica

MC-F-019. Tema 6.1. Neumática industrial: introducción a la neumática industrial.
MC-F-020. Tema 6.2. Neumática industrial: tratamiento de aire.
MC-F-021. Tema 6.3. Neumática industrial: generación y distribución de aire.
MC-F-022. Tema 6.4.1. Neumática industrial: actuadores neumáticos I.
MC-F-023. Tema 6.4.2. Neumática industrial: actuadores neumáticos II.
MC-F-024. Tema 6.4.3. Neumática industrial: actuadores neumáticos III.
MC-F-025. Tema 6.5. Neumática industrial: válvulas distribuidoras.
MC-F-026. Tema 6.6. Neumática industrial: regulación, control y bloqueo.
MC-F-027. Tema 6.7. Neumática industrial: detectores de señal.
MC-F-028. Tema 6.8. Neumática industrial: control de actuadores.
MC-F-029. Tema 6.9. Neumática industrial: diseño de circuitos.
MC-F-030. Tema 6.10. Neumática industrial: ciclos de operación.
MC-F-031. Tema 6.11. Neumática industrial: marcha-paro.
MC-F-032. Tema 6.12. Neumática industrial: electro-neumática.
MC-F-033. Tema 7.1. Hidráulica industrial: fluidos hidráulicos.
MC-F-034. Tema 7.2. Hidráulica industrial: elementos hidráulicos.
MC-F-035. Tema 7.3. Hidráulica industrial: bombas y motores hidráulicos.
MC-F-036. Tema 7.4. Hidráulica industrial: circuitos hidráulicos.
MC-F-037. Tema 8. Simbología neumática e hidráulica.

Ejercicios

ejercicios

Bloque I. Máquinas de fluidos incompresibles

EP-F-001. Problemas Tema 2. Bombas Centrífugas y Volumétricas.
EP-F-002. Problemas Tema 3. Turbinas Hidráulicas.

Bloque III. Neumática e hidráulica

EP-F-003. Problemas Tema 6. Neumática Industrial.

Otros Recursos

otros_recursos

OR-F-001. Presentación de la asignatura.

Pruebas de Evaluación

evaluacion

Criterios de evaluación

MÉTODOS DE EVALUACIÓN "SISTEMAS Y MÁQUINAS FLUIDO MECÁNICAS"
Descripción	Tipología	Evaluación final	Recuperación	%
Examen teórico-práctico de los Bloques I y II	Examen escrito	No	Sí	45%
Calificación mínima: 5,00. Duración: Fecha realización: Durante el cuatrimestre o en el periodo ordinario, en función del desarrollo de la asignatura. Condiciones de recuperación: En el examen extraordinario de septiembre. Observaciones:
Examen teórico-práctico del Bloque III	Examen escrito	No	Sí	40%
Calificación mínima: 5,00. Duración: Fecha realización: Durante el cuatrimestre o en el periodo ordinario, en función del desarrollo de la asignatura. Condiciones de recuperación: En el examen extraordinario de septiembre. Observaciones:
Memoria de prácticas de los Bloques I y II	Trabajo	No	No	5%
Calificación mínima: 0,00. Duración: Fecha de realización: Al finalizar las prácticas de los Bloques I y II. Condiciones recuperación: Observaciones: Para entregar una memoria de prácticas es obligatorio la asistencia a la misma con actitud positiva.
Memoria de prácticas del Bloque III	Trabajo	No	No	10%
Calificación mínima: 0,00. Duración: Fecha de realización: Al finalizar las prácticas del Bloque III. Condiciones recuperación: Observaciones: Para entregar una memoria de prácticas es obligatorio la asistencia a la misma con actitud positiva.
TOTAL				100%
OBSERVACIONES: La asistencia a clase (aula y laboratorio) exige actitud positiva (puntualidad, atención exclusiva a la clase...). No se guardan notas de partes de la asignatura para cursos posteriores.
OBSERVACIONES para alumnos/as a tiempo parcial: Los alumnos a tiempo parcial se evaluarán de la asignatura (100%) en un examen en la convocatoria ordinaria; el examen podrá contener partes teóricas, practicas y de laboratorio. De no superar la asignatura, la podrán recuperar en el examen extraordinario, en el que se volverá a evaluar de toda la asignatura.