Cálculo I (2011)
Diagrama de temas
-
Profesores
Elena Esperanza Álvarez Saiz
María Teresa Herrero Martínez
María Reyes Ruiz Cobo
Begoña Sánchez Madariaga
Joaquín García Ortiz
Departamento de Matemática Aplicada y Ciencias de la Computación

Asignatura básica de “Cálculo” de Primer Curso, en los Grados de la Escuela de Industriales y Telecomunicación de la Universidad de Cantabria, en el que se tratan los siguientes temas: números complejos, funciones reales de una variable real, sucesiones y series numéricas, series de potencias, funciones reales de varias variables, cálculo integral de funciones de una variable.
Palabras Clave de la Asignatura
Funciones de una Variable, Sucesiones Numéricas, Cálculo Infinitesimal, Funciones de Varias Variables, Números Complejos, Series de Potencias, Matlab, Derivabilidad, Integral de Riemann, Series Numéricas, Polinomios de Taylor.
-

Datos identificativos de la Asignatura
-
Asignatura: Cálculo I G272 / G281 / G319 / G404 / G413 / G422
-
Código: G272 / G281 / G319 / G404 / G413 / G422
-
Departamento / Área: Departamento de Matemática Aplicada y Ciencias de la Computación
-
Título: Grado en Ingeniería en Electrónica Industrial y Automática / Grado en Ingeniería de Tecnologías de Telecomunicación / Grado en Ingeniería Química / Grado en Ingeniería Eléctrica / Grado en Ingeniería en Tecnologías Industriales / Grado en Ingeniería Mecánica
-
Centro: Escuela Técnica Superior de Ingenieros Industriales y de Telecomunicación
-
Idioma de impartición: Español
-
Profesores responsables: Elena Álvarez Saiz, Begoña Sánchez Madariaga, Joaquín García Ortiz, María Teresa Herrero Martínez y María Esperanza Reyes Ruiz Cobo
Objetivos
-
Comprender y manejar los principales conceptos y herramientas básicas del cálculo diferencial de una y varias variables así como del cálculo integral de una variable.
-
Adquirir destrezas en la utilización de software matemático como ayuda en la resolución de problemas.
Programa de la asignatura
Bloque Temático I
-
Tema 1. Números complejos
-
Tema 1.1. Definición. Representación gráfica en el plano de Gauss. Formas de definir un número complejo.
-
-
- Tema 1.2. Operaciones elementales: adición, sustracción, producto, cociente, potencias y raíces.
-
Tema 2. Funciones reales de una variable real
-
Tema 2.1. Definición. Dominio e imagen. Gráficas de funciones elementales. Propiedades. Definición de continuidad.
-
Tema 2.2. Derivada en un punto: definición e interpretación geométrica. La derivada como razón de cambio. Cálculo de derivadas.
-
-
- Tema 2.3. Polinomios de Taylor. Definición. Fórmula de Taylor. Error de aproximación. Aplicaciones. Cálculo de extremos. Funciones equivalentes.
-
Tema 3. Funciones reales de una variable real
-
Tema 3.1. Definición de sucesión. Monotonía y acotación. Convergencia. Sucesiones equivalentes. Órdenes de infinitud.
-
Tema 3.2. Series de números reales. Carácter de una serie. Convergencia. Series de términos positivos. Series alternadas. Convergencia absoluta.
-
-
-
Tema 3.3. Series de potencias. Definición. Teorema de convergencia de una serie de potencias.
-
Bloque Temático II
-
Tema 4. Funciones reales de dos variables
-
Tema 4.1. Definición. Dominio e imagen. Trazas, curvas de nivel y gráfica.
-
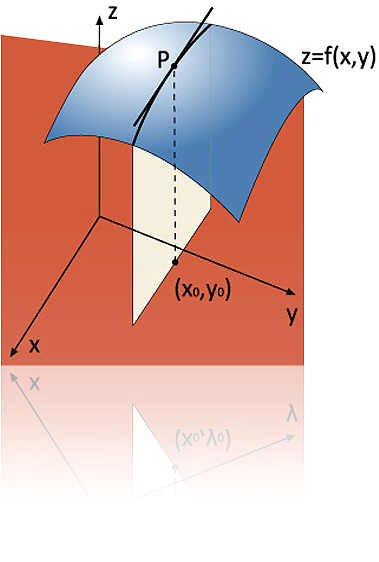
Tema 4.2. Derivada direccional: definición e interpretación geométrica. Derivadas parciales: definición, interpretación geométrica y cálculo. Derivadas parciales de orden superior. Función difrenciable. Plano tangente y recta normal. Gradiente.
-
-
- Tema 4.3. Polinomios de Taylor. Aproximación lineal. Extremos relativos de funciones diferenciables. Extremos condicionados. Método de los multiplicadores de Lagrange.
-
Tema 5. Cálculo integral de funciones de una variable
-
Tema 5.1. Primitiva. Métodos de integración.
-
Tema 5.2. Integral de Riemann. Funciones integrables. Teorema del valor medio. Teorema fundamental del cálculo integral. Regla de Barrow.
-
-
-

Básica
-
Bradley, G.L. & Smith, K.: «Calculo de una variable y cálculo de varias variables». Vol. I y II. Prentice Hall. ISBN: 84-89660-76-X.
-
Smith, R. & Minton, R.B.: «Cálculo». Vol. I y II. Editorial Mc Graw-Hill. ISBN: 84-481-3861-9.
-
Steward, J.: «Cálculo: conceptos y contextos». 3ª Ed. Thomson Learning. ISBN: 0-534-40986-5.
-
-

- MC-F-001. Prerrequisitos.
-
MC-F-002. Test inicial interactivo.
Resúmenes teóricos
-
MC-F-003. Tema 1. Números complejos.
- MC-F-004. Test interactivo del Tema 1.
-
MC-F-005. Tema 2. Funciones reales de una variable real.
- MC-F-006. Test interactivo del Tema 2.
-
MC-F-007. Tema 3. Sucesiones y Series Numéricas. Series de Potencias.
- MC-F-008. Test interactivo del Tema 3.
-
MC-F-009. Tema 4. Cálculo diferencial de funciones de varias variables.
- MC-F-010. Test interactivo del Tema 4.
Materiales complementarios
-

Prácticas de ordenador
- PR-F-001. Números reales y complejos.
- PR-F-002. Funciones de una variable.
- PR-F-003. Polinomios de Taylor.
- PR-F-004. Polinomios de Taylor: Acotación del resto.
- PR-F-005. Aproximación de la derivada.
- PR-F-006. Sucesiones numéricas.
- PR-F-007. Convergencia de series numéricas.
- PR-F-008. Gráficas de funciones de varias variables.
- PR-F-009. Derivación parcial. Gradiente.
- PR-F-010. Derivada direccional. Plano tangente.
- PR-F-011. Extremos de funciones de varias variables.
- PR-F-012. Integración de funciones reales.
-

Ejercicios propuestos
-
EP-F-001. Tema 1. Números complejos.
-
EP-F-002. Tema 2. Funciones reales de una variable real.
-
EP-F-003. Tema 3. Sucesiones y Series numéricas. Series de potencias.
-
EP-F-004. Tema 4. Cálculo diferencial de funciones de varias variables.
-
EP-F-005. Tema 5. Integración de funciones de una variable.
Ejercicios resueltos
-
-

Ejemplos de exámenes
Grado en Telecomunicaciones
Resto de Grados
Criterios de evaluación
- EG: Trabajo en grupo.
-
EV1: Evaluación del Bloque 1.
-
70% Prueba Escrita de los Temas 1, 2 y 3. Previsiblemente el día 22 de noviembre.
- 30% Actividades de evaluación de las Prácticas de Aula y de Laboratorio.
-
-
EV2: Evaluación del Bloque 2.
-
70% Prueba Escrita de los Temas 4 y 5. Previsiblemente el día 20 de enero.
- 30% Actividades de evaluación de las Prácticas de Aula y de Laboratorio.
-
- Nota: 0,1 · EG + 0,45 · EV1 - 0,45 · EV2.
-
Observaciones: Para aprobar la asignatura por Evaluación Continua se deberán cumplir los siguientes requisitos:
-
La media ponderada de EG, EV1 y EV2 es superior o igual a 5 sobre 10.
-
EV1 es superior o igual a 4 sobre 10.
-
EV2 es superior o igual a 4 sobre 10.
-
Se realicen al menos un 75% de las Actividades de Evaluación propuestas en EV1 y EV2.
-
-

 Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería Electrónica Industrial y Automática (G272) en formato PDF.
Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería Electrónica Industrial y Automática (G272) en formato PDF. Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería de Tecnologías de Telecomunicación (G281) en formato PDF.
Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería de Tecnologías de Telecomunicación (G281) en formato PDF. Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería Química (G319) en formato PDF.
Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería Química (G319) en formato PDF. Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería Eléctrica (G404) en formato PDF.
Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería Eléctrica (G404) en formato PDF. Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería en Tecnologías Industriales (G413) en formato PDF.
Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería en Tecnologías Industriales (G413) en formato PDF. Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería Mecánica (G422) en formato PDF.
Aquí puede descargarse la Guía de Aprendizaje del Grado en Ingeniería Mecánica (G422) en formato PDF.
-


Elena Esperanza Álvarez Saiz
Departamento de Matemática Aplicada y Ciencias de la Computación
UNIVERSIDAD DE CANTABRIA
Más información
María Reyes Ruiz Cobo
Departamento de Matemática Aplicada y Ciencias de la Computación
UNIVERSIDAD DE CANTABRIA
Más información
María Teresa Herrero Martínez
Departamento de Matemática Aplicada y Ciencias de la Computación
UNIVERSIDAD DE CANTABRIA
Más información
Begoña Sánchez Madariaga
Departamento de Matemática Aplicada y Ciencias de la Computación
UNIVERSIDAD DE CANTABRIA
Más información
Joaquín García Ortiz
Departamento de Matemática Aplicada y Ciencias de la Computación
UNIVERSIDAD DE CANTABRIA
Más información
Ángel Barón Caldera
Departamento de Matemática Aplicada y Ciencias de la Computación
UNIVERSIDAD DE CANTABRIA
Más información