Diagrama de temas

  • Álgebra y Geometría (2016-2019)

    Colapsar todo Expandir todo

              

     

     

    Profesores

    Jaime Gutiérrez Gutiérrez
    Ángel Barón Caldera
    Ana Isabel Gómez Pérez

    Departamento de Matemática Aplicada y Ciencias de la Computación

       

       

       

       

       

       

       

       

    Objetivos de la asignatura:

    • Resolver eficientemente sistemas de ecuaciones lineales. Aplicaciones a la ingeniería.

    • Manejar los conceptos de vectores, bases, subespacios. Conocer y entender las demostraciones del álgebra lineal y geometría.

    • Manejar con soltura las técnicas elementales del álgebra lineal y geometría.

    • Resolver y programar problemas de álgebra lineal y geometría, usando software matemático Sage.

    • Manejar la teoría del endomorfismo y alguna de sus aplicaciones.

    • Manejar los conceptos básicos de la geometría euclídea y afín.


    Palabras Clave de la Asignatura

    Cálculo Matricial, Álgebra Lineal, Espacio Vectorial, Espacio Afín Euclídeo, Fundamentos Matemáticos, Geometría, Ingeniería Eléctrica, Electrónica y Automática, Sage, Teoría del Endomorfismo.

     

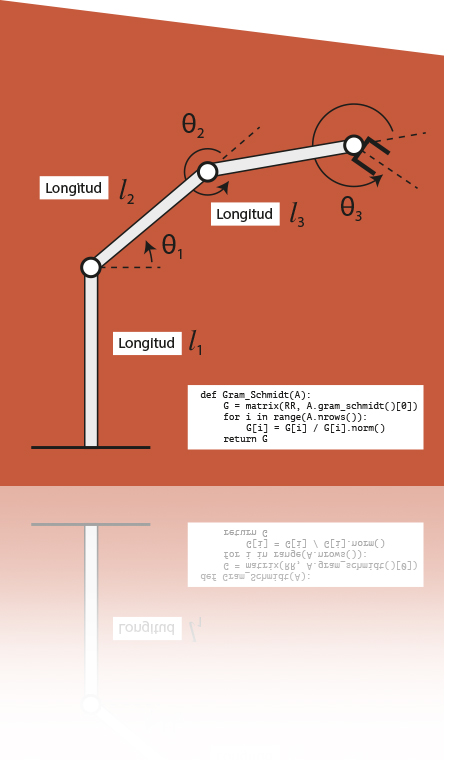
    * La figura de la portada es adaptación de una que aparece en el libro de David Cox, John Little & Donal O’Shea (2000): «Ideals, varieties, and algorithms». UTM, Springer Verlag.

  • Programa

     

     

    Datos identificativos de la Asignatura

    • Asignatura: Álgebra y Geometría

    • Código: G405/G273

    • Departamento / Área: Departamento de Matemática Aplicada y Ciencias de la Computación

    • Título: Grado en Ingeniería en Electrónica Industrial y Automática, Grado en ingeniería eléctrica

    • Centro: E.T.S de Ingenieros Industriales y de Telecomunicación

    • Créditos ECTS: 6

    • Idioma de impartición: Español

    • Profesores: Jaime Gutiérrez Gutiérrez / Ángel Barón Caldera / Ana Isabel Gómez Pérez



    Programa de la asignatura


    Tema I. Sistemas de Ecuaciones Lineales

    • 1.1 Sistemas de ecuaciones lineales

      • 1.1.1 Primeras definiciones y ejemplos: circuítos eléctricos, redes y grafos, circulación sobre una red vial, reacciones químicas.

      • 1.1.2 Sistemas homogéneos. El espacio vectorial K^m

      • 1.1.3 Eliminación Gaussiana

      • 1.1.4 Compatibilidad de los sistemas lineales. Teorema de Rouché- Frobenius. Teorema del rango

      • 1.1.5 Sistemas mal condicionados.

    • 1.2  Matrices

      • 1.2.1 Igualdad, suma, producto, matriz transpuesta, inversa y propiedades.

      • 1.2.2 Matrices y operaciones elementales

      • 1.2.3 Expresión matricula de una sistema lineal. Condición de una matriz.

      • 1.2.4. Factorización LU y  resolución de sistemas.

    • 1.3 Determinantes.

    • 1.4 Ejercicios propuestos

     

    Temático 2. Espacios Vectoriales

    • 2.1 Primeras definiciones y ejemplos

    • 2.2 Subespacios  vectoriales

    • 2.3 Dependencia e independencia lineal de vectores

    • 2.4 Bases de un espacio vectorial

    • 2.5 Coordenadas de un vector respecto de una base

    • 2.6 Dimensión de subespecios vectoriales. Teorema del rango. Suma directa.

    • 2.7 Ejercicios propuestos sobre espacios vectoriales.

     

    Tema 3. Aplicaciones lineales

    • 3.1 Concepto de homomorfismo

    • 3.2 Núcleo e imagen de un homomorfismo. Clasificación de homomorfismos.

    • 3.3 Operaciones con aplicaciones lineales

    • 3.4 Matriz asociada a una aplicación lineal

      • 3.4.1 Formas de definir una aplicación lineal

    • 3.5 Matrices de un homomorfismo asociadas a un cambio de bases

    • 3.6 Algunos homomorfismos particulares

    • 3.7 Ejercicios propuestos sobre aplicaciones lineales

      

    Tema 4. Teoría del Endomorfismo

    • 4.1 Valores y vectores propios

    • 4.2 Diagonalización de un endomorfismo

    • 4.3 Subespacios Invariantes. Teorema de Cayley-Hamilton

    • 4.4 Ejercicios propuestos de diagonalización de homomorfismos

      

    Tema 5. Espacio Vectorial Euclídeo

    • 5.1 Espacio vectorial Euclídeo

      • 5.1.1 Ortonormalización de Gram-Schmidt

      • 5.1.2 Espacios Ortogonales

      • 5.1.3 Proyección ortogonal

    • 5.2 Aplicaciones

      • 5.2.1 Aproximación por mínimos cuadrados

      • 5.2.2 Resolución de sistemas de ecuaciones sobredimensionados

      • 5.2.3 Factorización QR

    • 5.3 Isometrías

    • 5.4 Espacio Afín

      • 5.4.1 Sistemas de referencia o Sistemas de coordenadas

      • 5.4.2 Variedades afines o subespecio afín

      • 5.4.3 Rectas, planos e hiperplanos

      • 5.4.3 Aplicaciones Afines y movimientos

      • 5.4.4 Aplicaciones afines particulares

      • 5.4.5 La cinemática directa de un robot en el plano5.5 Ejercicios propuestos sobre Geometría Euclídea

    •  5.5 Ejercicios propuestos sobre Geometría Euclídea

  • Bibliografía

    bibliografia

     

     

     

    Libros y apuntes


     

    • F. Ayres. Matrices. McGraw-Hill, 1991.

    • S. Lipschutz. Álgebra Lineal. Serie de compendios Schaum. McGraw-Hill Interamericana de Espa~na,1992.

    • M. Queysanne, M. y A. Revuz. Geometría. CECSA,1976.

    • Una parte de los ejercicios de los temas en Materiales de Clase están recogidos o adaptados de: L. González Vega y C. Valero. Apuntes de Álgebra Lineal y Geometría. U. Cantabria, 2003.

    • W. Stein. Linear Algebra, 2013 http://wstein.org/courses/

      

     

    Software

  • Materiales de Clase

      

      

    • MC-F-001. Tema 1. Sistemas de Ecuaciones Lineales, Matrices y Determinantes.
    • MC-F-002. Tema 2. Espacios Vectoriales.
    • MC-F-003. Tema 3. Aplicaciones Lineales.
    • MC-F-004. Tema 4. Teoría del Endomorfismo.
    • MC-F-005. Tema 5. Geometría Euclídea.

  • Prácticas

     

     

  • Pruebas de Evaluación

     

     

    2015

     

    2016

     

    2017

    • PE-F-009. Examen final de junio

    • PE-F-010. Examen extraordinario de septiembre (con soluciones)

     

    2018

    • PE-F-011. Examen de evaluación continua (1)

    • PE-F-012. Examen de evaluación continua (2)

    • PE-F-013. Examen final de junio (1)

    • PE-F-014. Examen final de junio (2)

    • PE-F-015. Examen extraordinario de septiembre

     

    2019

      

    Examen tipo

     

     

  • Guía de aprendizaje

     

     

  • Sobre el Profesor

     

     

    logo UC

    Jaime Gutiérrez Gutiérrez

     

    Departamento de Matemática Aplicada y Ciencias de la Computación

    UNIVERSIDAD DE CANTABRIA
     
    Más información

     

    logo UC

    Ángel Barón Caldera

     

    Departamento de Matemática Aplicada y Ciencias de la Computación

    UNIVERSIDAD DE CANTABRIA
     
    Más información

     

    logo UC

    Ana Isabel Gómez Pérez

     

    Departamento de Matemática Aplicada y Ciencias de la Computación

    UNIVERSIDAD DE CANTABRIA
     
    Más información